CABLES SUBJECTED TO UNIFORMLY DISTRIBUTED LOAD
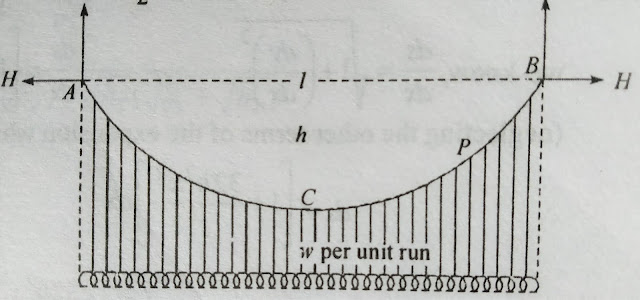
Consider a cable of span L, subjected to uniformly distributed load of w/m throughout the entire span. Let A and B are the two pinned supports which have the vertical reactions Va and Vb, horizontal reaction H at both the ends. Let h is the central dip (vertical distance) of the cable.
Due to symmetry, the reactions Va and Vb are equal
Therefore, Va = Vb = wL/2
Taking moment about point C to determine the horizontal thrust
Va (L/2) – H(h) -w(L/2) (L/4) = 0
(Note: The value of the moment is taken as zero, since the cable structure will always be free from moments)
(wL/2) (L/2) – H(h) -w(L/2) (L/4) = 0
Solving the above Eq
H = wL2/8h
Determination of tension forces
At supports: Since, there are two forces in each support.i.e., one vertical reaction and one horizontal reaction. Tension in the cable can be determined by calculating the resultant of the above forces
Tension at supports T = Resultant of V and H
T = √ (V2 +H2)
T = √ ((wL/2)2 +(wL2/8h)2)
Simplifying the above equation,
Therefore T = (wL/2) √ (1 +(L2/16h2))
Tension at center span of the cable = The total shear force at that span from either
of the support side
Shear force due to vertical load V = Va – w(L/2) = w(L/2) – w(L/2) = 0
Shear force due to Horizontal thrust = - H (Since it is in left direction hence taken
as negative)
= -wL2/8h
Total tension force at the center = T = √ (V2 +H2)
T = √ (02 +(-wL2/8h) 2)
Therefore, Tension force at center = T = H = wL2/8h
Hence by determining the tension at supports and center of span we can say that the tension force is always maximum at supports and minimum at center.
Therefore, Tmax = (wL/2) √ (1 +(L2/16h2))
Tmin = H = wL2/8h


0 Comments